堆中的路径

问题描述

给定n个数（无序），将n个数插入到一个小顶堆a[i]中，然后m个询问，给定一个下标x，打印a[x]到根节点的路径

题目链接:

https://pintia.cn/problem-sets/15/problems/713

数据范围:

N, M <= 1000

样例:

Input:

5 3
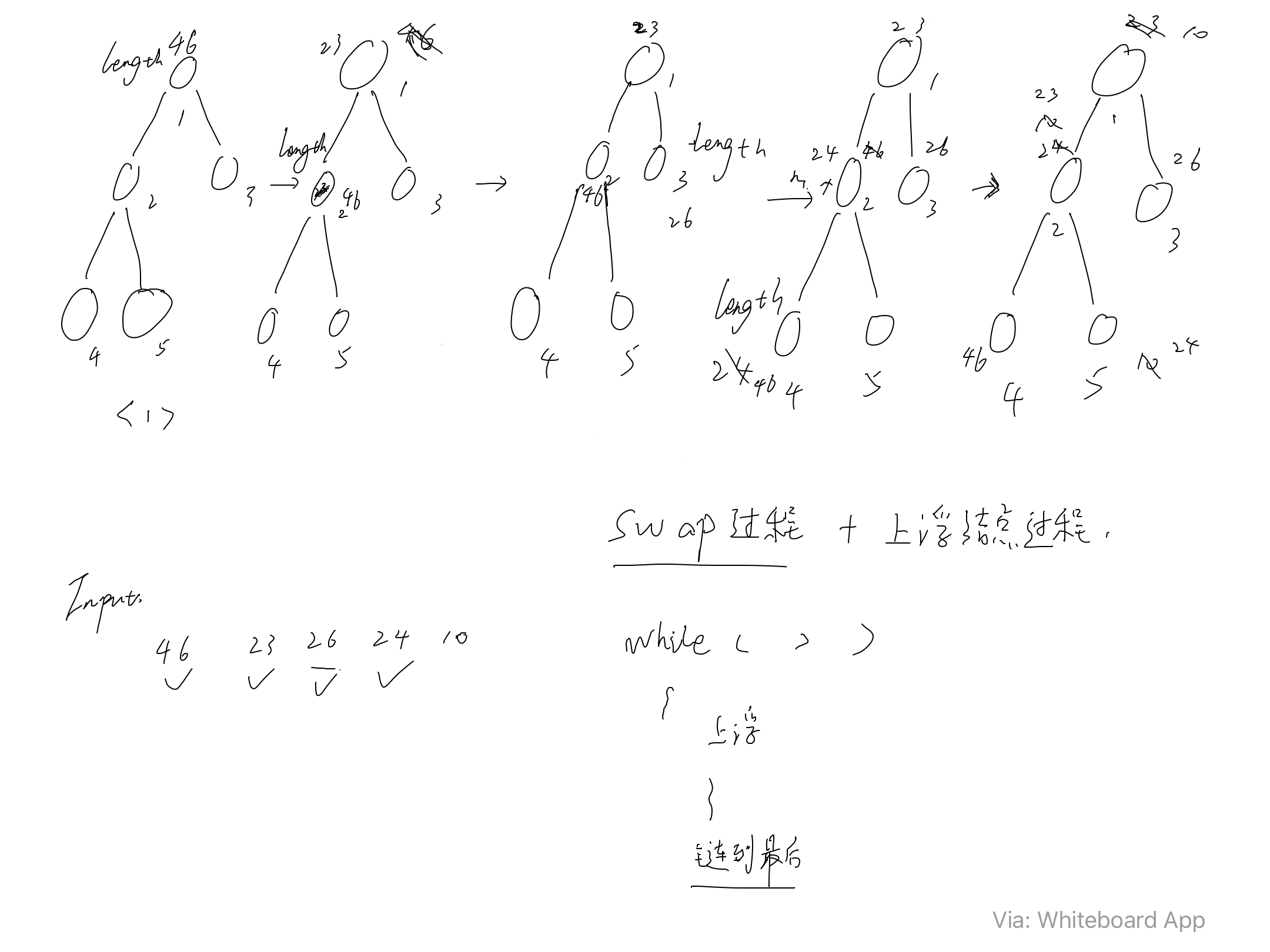
46 23 26 24 10
5 4 3

Output:

24 23 10
46 23 10
26 10

知识点

大顶堆小顶堆

1. 先根据序列的输入顺序构造出一颗完全二叉树（从1开始 用数组存储）

2. 大顶堆：arr[i + 1] >= arr[2i + 1] && arr[i] >= arr[2i + 2]

   小顶堆：arr[i + 1] <= arr[2i + 1] && arr[i] <= arr[2i + 2]

3. 建立大顶堆小顶堆的过程 == 堆排序的过程

   对结点来说： 上浮 下沉

4. 堆中的路径：

   

题目做法

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1000 + 10;
int arr[maxn];
int length;
void createminheap()
{
    arr[0] = -10001;
    length = 0;
}
void insertminheap(int x)
{
    length++;
    int n1 = length;
    while(arr[n1 / 2] > x)//把X放于最后逐个与它的父节点进行比较，很巧妙！
    {
        arr[n1] = arr[n1 / 2];
        n1 /= 2;
    }
    //小顶堆的上浮操作
    arr[n1] = x;//链到数组最后
}
int main(void)
{
    int n, m, x, temp = 0;
    cin >> n >> m;
    createminheap();
    for(int i = 0; i < n; i++)
    {
        scanf("%d", &x);
        insertminheap(x);
    }
    while(m--)
    {

        scanf("%d", &temp);
        printf("%d", arr[temp]);
        while(temp > 1)
        {
            temp /= 2;
            printf(" %d", arr[temp]);
        }
        printf("\n");
    }//格式注意~
    return  0;
}
//时间复杂度:O(N * logN)

总结点

1. 小顶堆和大顶堆的定义及构建方法。

2. 切入点不要去直接建立一个小顶堆 题意说明要插入，而不是去建立一个最小堆

参考资料

1.堆排序：https://www.cnblogs.com/lanhaicode/p/10546257.html

2.小顶堆的建立：https://blog.csdn.net/fdkNeverStopLearning/article/details/81662122