大四的萌新辣！

HDU-2795.Billboard

Posted on Edited on In Valine:

问题描述

有一个$h * w$的矩形，现在要在上边放置$n$个东西。东西的宽度为$w_i$。

放东西的原则是：

1.尽可能的在上层

2.尽可能放在左边

你要输出的是这$n$个东西在这个矩形的第几行。

输入

$n, w, n$ 其中 $1 <= h, w <= 10^9, 1 <= n <= 200,000$

下边又有$n$行数据，表示$w_i$, $1 <= w_i <= 10^9$

思路

我们可以画一下样例 ，如图所示

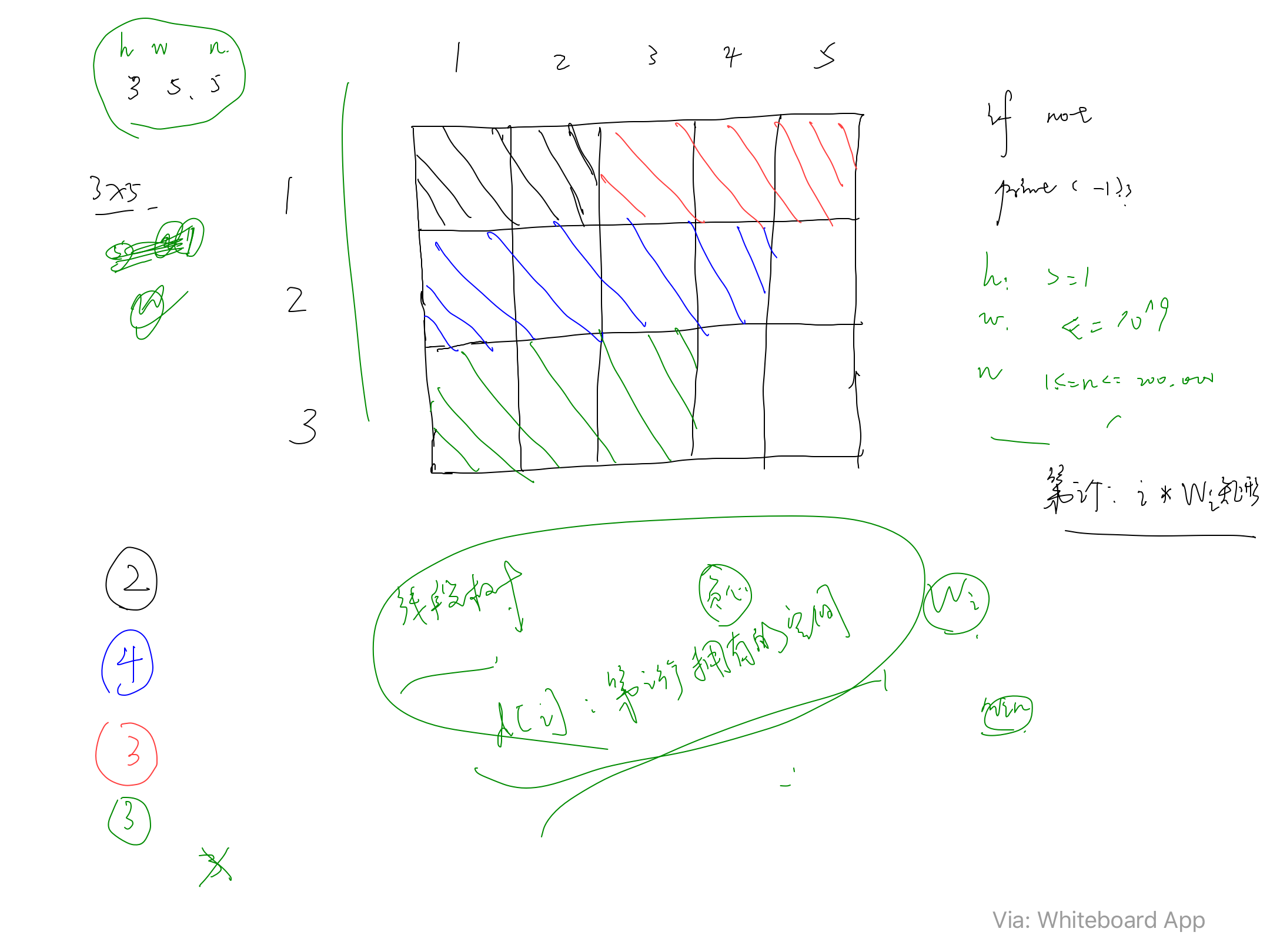
我们可以发现，对该矩形我们需要：

我们先不考虑全题，我们考虑局部。

对于区间$[l, r]$来说，左半边的最大值是$l_x$, 右半边的最大值是$r_x$。

  1. 如果一边是$>= w$，另一边不符合。我们直接选择即可。
  2. 如果两边都$<w$，那么我们可以直接输出$-1$。
  3. 如果两边都$>= w$,我们左右都可以放置，这样我们可以根据题目中的要求，选择左边。

简而言之，我们对于每一个$w_i$来说，都尽可能选择$h$较小且优先选择左边的。

询问的数据在$2*10^5$，$h$和$w$的范围是$1 <= h, w <= 10^9$，我们可以用线段树来维护这个矩形中每一行剩余的最大面积，对于每一个$w_i$,我们找到一个正确的行给它，并且用$ans$数组来记录所对应的行数。

我们可以搜改一体，找到之后，就修改这一行的最大面积(即结点存储的值)，并返回其位置。

现在就剩下最后一个问题了 对于数组空间 我们应该取什么样的值……

是根据$h$的范围，还是根据$n$的范围

我们看一下两个变量的范围 :

显然直接根据n的范围开数组一定会爆，我们考虑一下，

如果每行一个$w_i$,这样有可能高度达到$n$。那么最多也只有$2 * 10^5$个。

所以我们再开线段树空间的时候，最大开四倍的$n$即可。

我们建立的时候，直接比较$max(h, n)$即可。根据大的那一个建树。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
#include <bits/stdc++.h>
#define ll long long
#define IOS {ios::sync_with_stdio(false);cin.tie(0);}
using namespace std;
const int maxn = 200000 + 2;
ll h, w, n;
ll row;
ll d[maxn << 2], ans[maxn];//ans数组用来记录行数
void push_up(int rt)
{
    d[rt] = max(d[rt << 1], d[rt << 1 | 1]);
}
void build(int l, int r, int rt)
{
    if(l == r)
    {
        d[rt] = w;
        return ;
    }
    int m = (l + r) >> 1;
    build(l, m, rt << 1);
    build(m + 1, r, rt << 1 | 1);
    push_up(rt);
}
void update(int v, int l, int r, int rt)
{
    //v要更新的占用空间
    if(l == r)//找到合适的行数就是l
    {
        if(d[rt] >= v)//要考虑n == 1的情况！
        {
            d[rt] -= v;
            ans[row++] = l;
        }
        else
        {
            ans[row++] = -1;//当n 为1 时，没位置就存储1
        }
        return ;
    }
    int m = (l + r) >> 1;
    if(d[rt] >= v)//左右递归寻找
    {
        if(d[rt << 1] >= v)//递归尽量寻找上边的
            update(v, l, m, rt << 1);
        else
            update(v, m + 1, r, rt << 1 | 1);
    }
    else
    {
        ans[row++] = -1;
        return ;
    }
    push_up(rt);
}
int main(void)
{
    IOS
    while(cin >> h >> w >> n)
    {
        memset(d, 0, sizeof(d));
        memset(ans, 0, sizeof(ans));
        row = 0;
        if(h > n)
            h = n;
        build(1, h, 1);
        for(int i = 1; i <= n; i++)
        {
            int x;
            cin >> x;
            update(x, 1, h, 1);//单点更新
        }
        for(int i = 0; i < row; i++)
            cout << ans[i] << endl;
    }
    return 0;
}

注意点

  1. 单点更新时变量的变化逻辑关系

  2. 搜改一体的具体操作细节见代码

  3. 提供一个构造特例：

    input:

    1
    2
    5 2 1
    5

    output:

    1
    -1