大四的萌新辣！

Codeforces Round #631(Div. 2)

Posted on Edited on In Valine:

菜鸡的$div2$补题现场……

A:Dreamoon and Ranking Collection

1.题目描述：

给你一个$n$和$x$,然后有$n$个数据,这个人从$1$开始比赛，$n$组数据包含着这个人进行的比赛，未进行的比赛可以用$x$补全，但$x$也要相应$-1$

问：他能够到达的最大比赛次数是多少？

input:

1
2
3
4
5
6
7
8
9
10
11
5
6 2
3 1 1 5 7 10
1 100
100
11 1
1 1 1 1 1 1 1 1 1 1 1
1 1
1
4 57
80 60 40 20

output:

1
2
3
4
5
5
101
2
2
60

2.思路

我们可以从$1$开始往后扫一边，对应的$ans += 1$,如果这个地方是空，我们给他填上，并且$x$相应$-1$，直到$x == 0$，看此时的$ans$就是我们可以得到的最大的比赛值。

这里存储的是每一场比赛对应的值，我们可以用一个$map$来存储。

注意：

  • 变量全局定义，记得初始化。
  • $for$循环的判断条件
  • $map$的清空[不然多组样例会wa掉]

3.代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
/**
* Copyright(c)
* Author : tiketiskte
*/
#include <bits/stdc++.h>
#define IOS {ios::sync_with_stdio(false);cin.tie(0);}
#define ll long long
#define INF 0x3f3f3f3f
 
using namespace std;
const int maxn = 100 + 5;
int t, n, x, temp,cnt;
int main()
{
   IOS
   cin >> t;
   while(t--) {
       n = x = temp = cnt = 0;
       map<int, int>mp;
       cin >> n >> x;
       for(int i = 1; i <= n; i++) {
           cin >> temp;
           mp[temp] = 1;
       }
       /* for(int i = 1; i <= n; i++) {
           cout << mp[i] << endl;
       } */
       for(int i = 1; ; i++) {
           if(x == 0) {
               break;
           }
           if(mp[i] == 0) {
               //cout << "#1:" << x << endl;
               x -= 1;
               mp[i] = 1;
               //cout << "#2:" << x << endl;
           }
       }
       /* for(int i = 1; i <= n; i++) {
           cout << mp[i] << endl;
       } */
       for(int i = 1; mp[i] != 0; i++) {
           //cout << mp[i] << endl;
           cnt++;
       }
       cout << cnt << endl;
   }
   //system("pause");
   return 0;
}

B:Dreamoon Likes Permutations

1.题目描述

定义一个$permutation$,如果对于一个序列，包含了从$1$到$n$的每一项，则该序列称为$permutation$.

有两个符合$permutation$的序列$p1, p2$, 长度分别为$l1, l2$。现在连接成为一个长度为$l1 + l2$的序列$a$，第一个$l1$元素是$p1$， 下一个$l2$元素是$p2$.

现在给你一个序列$a$，让你找两个符合$permutation$的序列$p1， p2$，找到还原它们的所有方法。

输出存在的方法并输出$p1$ 和 $p2$的长度.

input:

1
2
3
4
5
6
7
8
9
10
11
12
13
6
5
1 4 3 2 1
6
2 4 1 3 2 1
4
2 1 1 3
4
1 3 3 1
12
2 1 3 4 5 6 7 8 9 1 10 2
3
1 1 1

output:

1
2
3
4
5
6
7
8
9
10
2
1 4
4 1
1
4 2
0
0
1
2 10
0

2.思路：

u1s1，一开始看到题意有点懵，读了两遍题，才大致了解了一下。

我们可以想一下，对于一个序列，如果它是符合$permutation$这个条件的，则其最大值我们设定是$ma$，如果$a$序列可以分割，则其最大值为$max(len1, len2)$

所以会有两种解决方案：

  • $len1 = ma, len2 = n - ma$
  • $len1 = n - ma, len2 = ma$

我们只需要检查这两种分割方式是否符合$permutation$即可。

我们可以用一个标记数组$vis$来判断该序列从$1$到$len1$是否全部出现即可。

注意 ：序列两部分的断点 ，不要去考虑原数组，只需要考虑$vis$是否符合$permutation$即可。

提供一组样例：【需要特判！！！】

input:

1
1 2 3 3 2 1

output:

1
3

3.代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
/**
* Copyright(c)
* Author : tiketiskte
*/
#include <bits/stdc++.h>
#define IOS {ios::sync_with_stdio(false);cin.tie(0);}
#define ll long long
#define INF 0x3f3f3f3f

using namespace std;
const int maxn = 200000 + 5;
int t, n;
int a[maxn], vis[maxn], ans[maxn][2];
bool check(int l1, int l2) {
    for(int i = 1; i <= n; i++) {
        vis[i] = 0;
    }
    for(int i = 1; i <= l1; i++) {
        vis[a[i]] = 1;
    }
    for(int i = 1; i <= l1; i++) {
        if(vis[i] == 0) {
            return 0;
        }
    }
    for(int i = 1; i <= n; i++) {
        vis[i] = 0;
    }
    for(int i = l1 + 1; i <= n; i++) {
        vis[a[i]] = 1;
    }
    for(int i = 1; i <= l2; i++) {
        if(vis[i] == 0) {
            return 0;
        }
    }
    return 1;
}
int main()
{
   IOS
   cin >> t;
   while(t--) {
       int ma = -1;
       memset(a, 0, sizeof(a));
       memset(vis, 0, sizeof(vis));
       memset(ans, 0, sizeof(ans));
       cin >> n;
       for(int i = 1; i <= n; i++) {
           cin >> a[i];
           ma = max(ma, a[i]);
       }
       int cnt = 0;
       if(check(ma, n - ma)) {
           cnt++;
           ans[cnt][0] = ma;
           ans[cnt][1] = n - ma;
       }
       if(ma * 2 != n && check(n - ma, ma)) { //判重复方案
           cnt++;
           ans[cnt][0] = n - ma;
           ans[cnt][1] = ma;
       }
       cout << cnt << endl;
       for(int i = 1; i <= cnt; i++) {
           cout << ans[i][0] << " " << ans[i][1] << endl; 
       }
   }
   system("pause");
   return 0;
}

C. Dreamoon Likes Coloring

1.题目描述

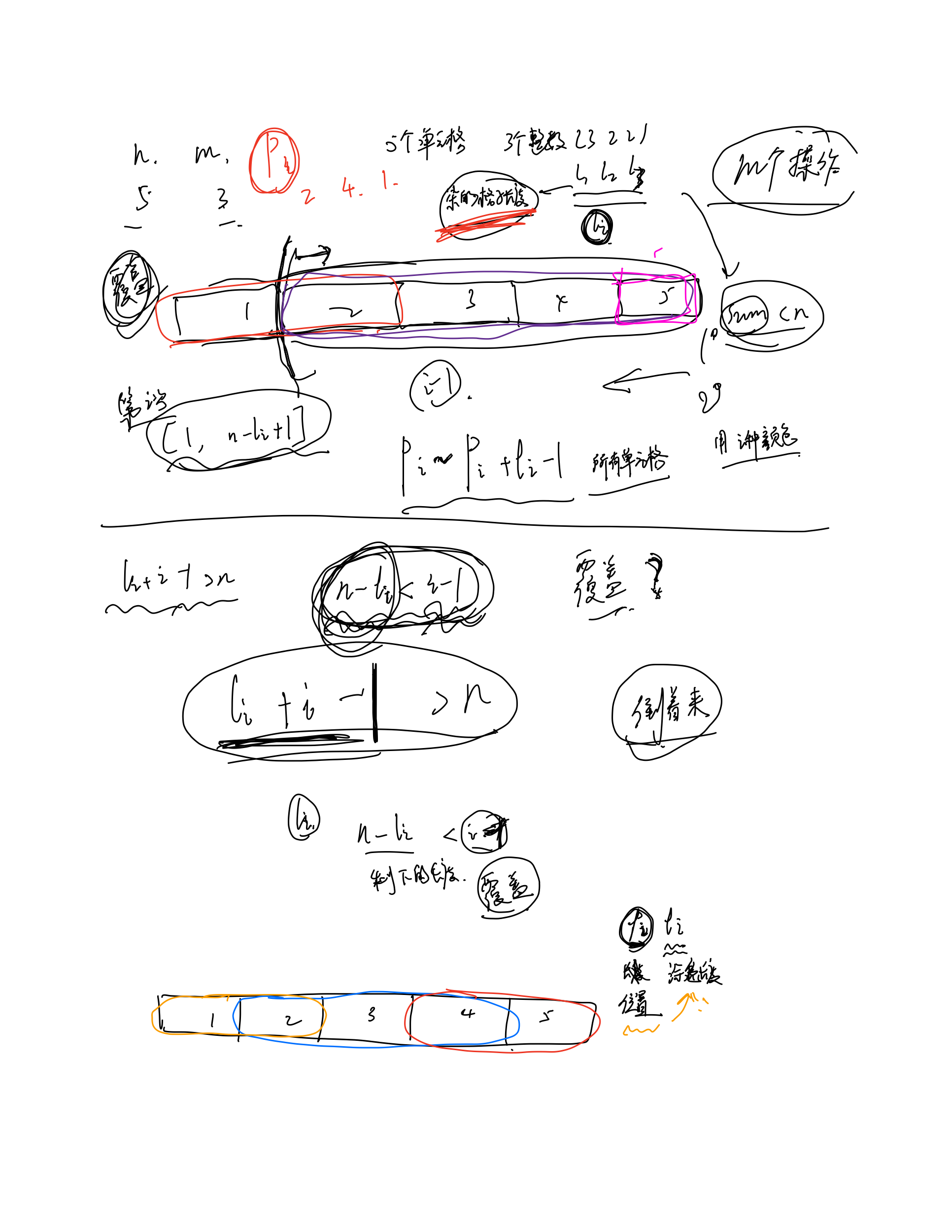
给你一个长度为$n$的长条单元格让你涂色，可以进行$m$次涂色操作，分别给定$l_1, l_2, \ldots, l_m$。

对第$i$次操作，你可以选择一个$p_i$在$[1, n - l_i + 1]$ 范围内，并对$p_i$到$p_i + l_i -1$所有的单元格进行涂色。后来涂色的单元格颜色可以覆盖之前进行的涂色。

你的任务：在$m$次操作后：

  • 所有的颜色出现一次
  • 并所有单元格都有颜色。[即有m种颜色…..]

input：

1
2
3
4
5
6
first:
5 3
3 2 2
second:
10 1
1

output：

1
2
3
4
first:
2 4 1
second:
-1

2.思路：

乱搞图片…

[规范解答]【感觉有点难以理解】靠……

我们首先考虑可能输出$-1$的情况，类似这种题目，我们先寻找可能不满足的条件，再寻找解决方案。

  • 设$m$次涂色的单元格长度之和$sum$ ，当$sum < n$时，显然不满足第二种条件，不能涂满整个单元格长条。
  • 对任意$i$,要满足$l_i + i - 1 > n$，即如果$n - l_i < i - 1$，那么我们进行完$i$次操作后，只有$n - l_i$个单元格没有被第$i$中颜色着色。所以进行完之后，至少$i - 1$种以前的颜色会消失。

我们要找到的就是涂色的位置$pos$。

[贪心做法]

我们与上边的第一种条件一样，先加起来，如果$sum < n$那么一定不成立。

然后我们采取一种贪心方式来涂，保证从第一次涂开始，操作尽可能小比并且涂满。

然后我们每一种颜色的长度缩小，这取决于$sum$的大小，然后更新$pos$和$sum$.

当$l_i+pos-1>n$时，如果我们从$pos$开始涂色，那么颜色的末尾就会超过$n$，所以我们必须在$pos$之前涂色。

但我们前边的操作保证是最小解，所以该操作会覆盖掉前边的方案，不成立。

3.代码：

[做法1]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
/**
* Copyright(c)
* Author : tiketiskte
*/
#include <bits/stdc++.h>
#define IOS {ios::sync_with_stdio(false);cin.tie(0);}
#define ll long long
#define INF 0x3f3f3f3f

using namespace std;
const int maxn = 100000 + 5;
int n, m;
int a[maxn];
ll p[maxn];
int main()
{
   IOS
   cin >> n >> m;
   for(int i = 1; i <= m; i++) {
      cin >> a[i];
      if(a[i] + i - 1 > n) {
         puts("-1");
         return 0;
      }
   }
   for(int i = m; i > 0; i--) {
      p[i] = p[i + 1] + a[i];
   }
   if(p[1] < n) {
      puts("-1");
      return 0;
   }
   for(int i = 1; i <= m; i++) {
      //cout << max((ll)i, n - p[i] + 1);
      printf("%lld", max((ll)i, n - p[i] + 1));//玄学错误 cout wa掉
      if(i < m) {
        putchar(' ');
      }
      else {
         puts("");
      }
   }
   //system("pause");
   return 0;
}

[做法2]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
/**
* Copyright(c)
* Author : tiketiskte
*/
#include <bits/stdc++.h>
#define IOS {ios::sync_with_stdio(false);cin.tie(0);}
#define ll long long
#define INF 0x3f3f3f3f

using namespace std;
const int maxn = 100000 + 5;
int n, m, pos;
ll sum;//注意爆数据范围！！！
int a[maxn], ans[maxn];
bool flag;
int main()
{
   IOS
   cin >> n >> m;
   for(int i = 1; i <= m; i++) {
      cin >> a[i];
      sum += a[i];
   }
   if(sum < n) {
      cout << "-1" << endl;
      return 0;
   }
   pos = 1;
   sum -= n;
   flag = false;
   for(int i = 1; i <= m; i++) {
      if(a[i] + pos - 1 > n) {
         flag = 1;
         break;
      }
      if(sum >= a[i]) {//贪心选择最小范围
         sum -= a[i] - 1;
         a[i] = 1;
      } else {
         a[i] -= sum;
         sum = 0;
      }
      ans[i] = pos;
      pos += a[i];
   }
   if(flag) {
      cout << "-1" << endl;
   } else {
      for(int i = 1; i < m; i++) {
         cout << ans[i] << " ";
      }
      cout << ans[m] << endl;
   }
   //system("pause");
   return 0;
}